Using muons to determine the role of Hydrogen impurity in oxides

By Rui Vilao

Transistors are key components of computer chips. Our ability to develop transistors of ever-decreasing size underpins the future of computing, if it is to follow Moore´s law for any longer. However, transistor miniaturisation is currently facing fundamental obstacles as these components reach atomic dimensions. One of the problems faced by transistor science is the thickness of the insulator layer of silicon dioxide SiO2 used in the gate of transistors. In today´s transistors, this insulator layer is only nanometers thick.

This means that it can be conductive even when very low tensions are applied and this can prevent the device from operating. The capacity of insulators to respond to an applied electric field can be quantified in a parameter called the dielectric constant. A possible solution to the problem of insulator thickness is the replacement of SiO2 by more ‘robust’ insulators with a higher dielectric constant. Oxides with high dielectric constants are therefore currently under intense scrutiny. In this context, the investigation of the role hydrogen as an impurity has become increasingly important, especially since the discovery that this ubiquitous impurity may play a role in electron conductivity in zinc oxide ZnO.

Theoretical schemes have also been proposed to explain the behaviour of hydrogen as an electrically active impurity or as an amphoteric impurity.
We have recently addressed the characterisation of the isolated hydrogen configurations in the semiconducting oxide α- TeO2 (paratellurite), a most interesting and relevant semiconducting oxide among nonlinear optical materials [1]. α- TeO2 is a promising active material for optical devices and presents a relatively high dielectric constant. The presence of hydrogen in the fabrication process of this material leads to hydrogen incorporation in the lattice, and we were interested in investigating the effects of the incorporation of the isolated hydrogen impurity in the electrical properties of this material.

Vilao Figure 1. The basic muon spin rotation experiment. On the left, the basic setup: spin-polarised positive muons are implanted into a sample, in a region subject to a magnetic field Ba perpendicular to the initial muon spin, surrounded by two positron detectors in the forward (F) and backward (B) direction. The asymmetric probability for positron emission rotates with the muon spin and is drawn for three different times. The positrons counts NB and NF detected by detectors F and B form histograms like those shown in the right side. The experimental asymmetry A=(NB-NF)/( NB+NF) is shown as an inset.

Figure 1.

From the experimental point of view, the use of muonium, an atom composed of a positive muon as the nucleus [Mu≡µ+e_], as a light pseudo-isotope of hydrogen has become standard in order to obtain information about the electronic states of hydrogen in materials. The respective results compare well with those obtained with protons, for the very few cases allowing comparison. We have thus performed muon-spin research (µSR) experiments at the EMU instrument of the ISIS Facility, Rutherford Appleton Laboratory, United Kingdom, and at the DOLLY instrument of the Muon Spin Laboratory at the Paul Scherrer Institut, Switzerland. Our colleague Apostolos Marinopoulos in Coimbra has performed the corresponding first-principle (ab-initio) calculations.

Vilao Figure 2. Muon spin asymmetry as a function of time, in transverse geometry (B = 1.5 mT), at T = 5 K (below), and at T = 300 K (observed at PSI). A clear nearly undamped oscillation at the Larmor frequency. A strongly relaxed signal is also observed in the first few hundred nanoseconds.

Figure 2.

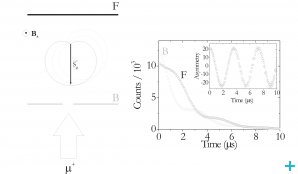
In the muon spin rotation measurements, a nearly 100% spin-polarised beam of positive muons, with their spin antiparallel to their momentum (Figure 1) was directed at a TeO2 single crystal while a magnetic field was applied perpendicularly to the muon spin, as illustrated in Figure 1. These experiments take advantage not only of the possibility of producing muon beams with full spin polarisation (all the muon spins pointing in the same initial direction) but also of the fact that the muon decay into a positron has the positron emitted preferentially in the direction of the muon spin. The follow-up of the evolution of the pattern of emitted positrons thus allows to have a direct link to the corresponding evolution of the muon spin and magnetic momentum, turning the muon into a precise magnetometer in condensed matter. In their thermalisation process, muons can capture an electron and form muonium. In this exotic atomic species, the muon spin interacts very strongly with the electron spin through the so-called hyperfine interaction, yielding typical frequency patterns. We could identify the muonium configurations involved through the corresponding frequency patterns. Further information about the muonium atom location and dynamics could be extracted from the relaxation of the muon spin polarisation, as well as from temperature dependence studies.

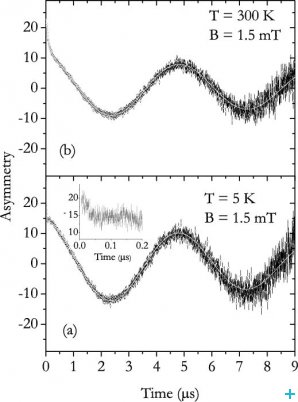
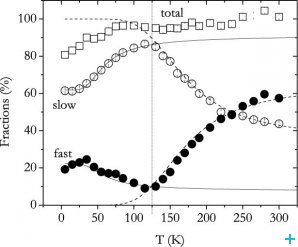
As shown in Figure 2, we observed two components with distinct spin relaxation rates, named fast and slow in the time spectra. The temperature dependence study revealed that a conversion process of the muonium states present is suggested by the fractions (Figure 3). We associated the low-temperature behaviour of the relaxation of the slow component (Figure 4) to the formation of a shallowly-bound muonium atom, with a hyperfine interaction of only about a few hundred kHz. In order to obtain a precise value for the hyperfine interaction A associated to the fast component identified at low temperatures, we performed an experiment with the applied field parallel to the initial muon spin polarisation. The dependence of the muon spin polarisation with the strength of the external applied field allowed us to determine the value A = 3.5 GHz (Figure 5).

Figures 3,4 and 5

The slow and fast fractions identified were assigned to a shallow-donor configuration at an oxygen-bound site and to a deep-acceptor configuration at an interstitial site, respectively. In the shallow donor configuration, an electron is suggested to be bound to the muon with an extremely small ionization energy of only about 6 meV, so that this centre effectively contributes with electrons to the conduction band and to n-type conductivity. In contrast, the deep acceptor configuration corresponds to an atomic-like muonium centre where the electron is tightly bound with and ionization energy of the order of the eV. The temperature dynamics is likely to correspond to delayed electron capture by the deep-acceptor muonium, forming the negatively charged state Mu― [1]. This centre thus tends to behave as an acceptor, removing electrons and contributing to p-type conductivity.

The present experimental results, in association with the ab initio calculations, clearly identify the basic donor and acceptor configurations of isolated hydrogen in TeO2. Moreover, the corresponding levels are suggested to be inverted in the band gap, so that the binding energy of the second electron in the H- configuration is larger than the binding energy of the electron in the H0 configuration. As a consequence of this inversion of levels, if the material is electron-deficient (p-type), hydrogen will tend to donate its electron to the conduction band, acting as a donor. If the material is electron rich (n-type), hydrogen will tend to capture an extra electron from the conduction band, behaving as an acceptor. In short, hydrogen will tend to always counteract the prevailing conductivity, and to act as an amphoteric impurity.

Reference:
[1] R. C. Vilão, A. G. Marinopoulos, R. B. L. Vieira, A. Weidinger, H. V. Alberto, J. Piroto Duarte, J. M. Gil, J. S. Lord and S. F. J. Cox, Hydrogen impurity in paratellurite α-TeO2: Muon-spin rotation and ab initio studies, Phys. Rev. 84, 045201 (2011)

R. C. Vilão is an Assistant Professor at the Department of Physics of the University of Coimbra. He is a member of the Group of electronic and magnetic properties of materials at the Centre for Materials Research by X-ray diffraction.