Method to investigate structure: Diffraction
Browse the tabs to learn about techniques and the facilities where you can find them
Overview
Neutrons are diffracted by solids, especially crystals. Neutron Diffraction is a useful tool to identify structures.

We have a Special Feature that explains these techniques and where they are used. Picture courtesy of the Oak Ridge National Laboratory.
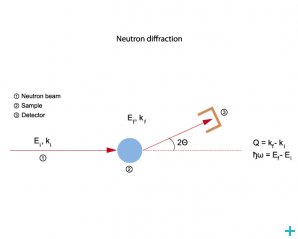
Neutron diffraction or elastic neutron scattering is the application of neutron scattering to the determination of the atomic and/or magnetic structure of a material: A sample to be examined is placed in a beam of thermal, hot or cold neutrons to obtain a diffraction pattern that provides information of the structure of the material.
The technique is similar to X-ray diffraction but due to the different scattering properties of neutrons versus x-rays, complementary information can be obtained. In particular, neutron diffraction is advantageous for the localisation of light atoms and the determination of magnetic ordering.
Neutron diffraction principle
Neutron diffraction has some unique characteristics when compared to other types of radiation. This makes it very useful for the study of the atomic structure of liquids, amorphous materials and crystalline materials.
Diffraction can see the ordered part of systems, which means, for ordered systems (crystals), their average structure but also deviations from this perfect order; for disordered systems, the ordered portions existing amid this disorder.
Diffraction methods can be divided into two interactions, nuclear diffraction: diffraction due to the interaction between neutrons and atomic nuclei, and magnetic diffraction: diffraction due to the interaction between the magnetic moments of neutrons and magnetic moments of atoms.
Bragg equation
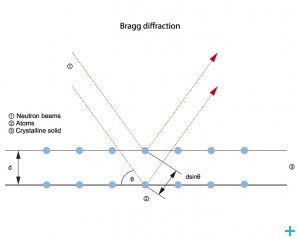
The measurement principle of neutron diffraction is based on the Bragg Equation. Bragg diffraction occurs when electromagnetic radiation or subatomic particle waves with wavelength comparable to atomic spacings are incident upon a crystalline sample, are scattered in a specular fashion by the atoms in the system, and undergo constructive interference in accordance to Bragg's law.
For a crystalline solid, the waves are scattered from lattice planes separated by the interplanar distance d. Where the scattered waves interfere constructively, they remain in phase since the path length of each wave is equal to an integer multiple of the wavelength. The path difference between two waves undergoing constructive interference is given by 2dsinθ, where θ is the scattering angle.
This leads to Bragg's law, which describes the condition for constructive interference from successive crystallographic planes of the crystalline lattice:
2d·sin(θ)=nλ
Where n is an integer determined by the order given, and λ is the wavelength.
Diffraction methods and their applications:
- Refinement of crystallographic or magnetic structure on polycrystalline materials
- Phase transformations and reaction pathways as a function of external parameters (temperature, magnetic or electric field, mechanical strain or pressure)
- Refinement of crystallographic or magnetic structure on polycrystalline materials
- Structure solution on complex systems or proteins
Strain/ texture analysis:
- Analysis of residual strain on engineering materials
- Analysis of texture on engineering materials
(Can be found at BER II , NPL.)
Diffuse scattering:
- Investigation of non-crystalline structures: liquids, amorphous materials
- Disorder and short-range in crystals
Neutron Optics Diffraction
(Can be found at NPL)
Further reading
- Crespo, I., From Bragg’s law to neutron diffraction, NMI3 article
- Furrer A., Mesot J., Strässle T. (2009) Neutron Scattering in Condensed Matter Physics (World Scientific)